화폐의 시간 가치(TVM)는 금융의 가장 기본적인 개념 중 하나입니다. 화폐의 시간 가치의 기본 원칙은 오늘 당신의 손에 있는 루피가 미래에 받게 될 동일한 루피보다 더 가치가 있다는 것입니다.
예를 들어- 오늘 100만 루피 또는 내년 같은 금액 중에서 선택할 수 있는 옵션이 제공된다면 무엇을 선택하시겠습니까?
귀하의 답변은 오늘 100만 루피가 될 것이라고 확신합니다.
왜요? 내년에 내가 당신에게 100만 루피를 줄 것이라는 것을 당신이 믿지 않기 때문입니다. 따라서 제안이 아직 제공되는 동안 기회를 잡고 오늘 100억 루피를 가져가려고 생각할 수 있습니다. 맞나요?...농담!!
오늘 사용할 수 있는 돈이 잠재적인 수입 능력으로 인해 미래에 얻을 수 있는 동일한 돈에 비해 가치가 더 높기 때문에 여기에서 Rs 1Crore를 선택해야 합니다.
돈은 시간이 지남에 따라 성장할 가능성이 있습니다. 이자를 받을 수 있습니다.
<노스크립트>
예를 들어, 연 5%의 이자를 주는 저축 계좌에 오늘 100억 루피를 예치하면 순 가치는 내년에 105억 루피가 됩니다. 요컨대, 추가로 Rs 5 lakh를 벌게 됩니다.
이러한 잠재적인 수입 능력 때문에 오늘 수중에 있는 돈이 내일 받는 돈보다 더 가치가 있습니다.
목차
이제 화폐의 시간 가치 개념을 이해했으므로 화폐의 미래 가치를 찾는 데 사용되는 기본 공식이 있습니다.
여기,
FV =화폐의 미래 가치
PV=화폐의 현재 가치
나 =이자율
t=년 수
위의 공식은 이자율과 기간이 주어졌을 때 미래의 현재 가치의 가치가 얼마인지 구하는 데 사용됩니다. 예시를 통해 더 자세히 이해해 보겠습니다.
예시 1:이자율이 연 10%인 경우 1년 후 Rs 20 lakh의 미래 가치는 얼마입니까?
여기에서 PV =Rs 20,00,000; 나는 =0.10; t=1
방정식 1 사용:
<노스크립트>
FV =PV * (1 + i) ^t =20,00,000(1+0.10) =22,00,000
따라서 10%의 이율로 1년 후 Rs 20 lakhs의 미래 가치는 Rs 22 lakhs가 됩니다.
또한 방정식-1을 변경하여 현재 가치(PV)를 찾을 수도 있습니다(이자율과 기간이 주어진 경우).
화폐의 현재 가치의 방정식은 다음과 같습니다.
<노스크립트>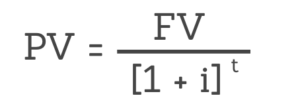
화폐의 미래가치, 이자율, 기간을 고려하여 화폐의 현재가치를 구하는 문제를 풀어봅시다.
예시 2:이자율이 연 10%인 경우 3년 후 지불해야 하는 Rs.5,000의 현재 가치는 얼마입니까?
여기서 FV=5,000; i=10%; t=3
PV =5000/ (1.10)^3 =Rs.3756.57
따라서 현재 가치는 Rs 3,756.57입니다.
즉, 3,756.57루피가 연 10%의 금리라면 3년 후 5,000루피의 미래 가치가 됩니다.
시간과 이자 외에 화폐의 미래 가치에 영향을 미치는 세 번째 요소도 있습니다. 복리 빈도/기간입니다.
복리 기간은 TVM 계산에 큰 영향을 미칩니다. 예제를 통해 이것을 이해합시다.
화폐의 현재 가치(PV) =Rs 10,00,000
이자율(i) =10%
년 수(t) =1
요약사항: 주어진 복리 기간(n) 동안 FV 공식은 다음과 같습니다.
FV =PV * (1 + i/n) ^t*n
여기서:n=연간 복리 기간 수
여기에서는 다양한 시나리오에서 금액이 연간, 분기별, 월별 및 일일 복리화되는 4가지 시나리오를 고려할 것입니다.
시나리오 1:매년 복합
FV =10,00,000 [ 1 + 0.1] ^1 =11,00,000
시나리오 2:1년에 4번 복합
FV =10,00,000 [ 1 + (0.1/4)] ^1*4 =11,03,813
시나리오 3:1년에 12번 합성
FV =10,00,000 [ 1 + (0.1/12)] ^1*12 =11,04,713
시나리오 4:1년 동안 매일 합성
FV =10,00,000 [ 1 + 0.1/365] ^1*365 =11,05,156
위의 4가지 시나리오에서 1년 동안 매일 복리화폐가 지급되는 시나리오 4에서 미래 가치가 가장 높다는 것을 알 수 있습니다.
분명히, 화폐의 미래 가치는 복리 빈도에 따라 증가합니다.
배당주에 투자할 기회가 있다고 가정해 보십시오.
이 주식은 주주들에게 배당금을 제공한 좋은 과거 기록이 있으며 향후 4년 동안 연간 10루피의 일관된 배당금을 제공할 것이라고 안전하게 결론지을 수 있습니다.
또한 4년차 말에 해당 주식을 Rs 500의 가격에 판매할 수 있을 것이라고 예측했습니다. 또한 여기에서 연간 15%의 투자 수익을 원합니다.
화폐의 시간가치 개념을 이용하여 구매가격을 계산할 수 있습니다.
여기에서 1년부터 4년까지 미래에 받게 될 모든 돈의 가치를 이미 알고 있습니다. 다음에 해야 할 일은 미래에 얻게 될 이 모든 돈의 현재 가치를 찾아 더하는 것입니다. 위로.
순가가 주식의 시장 가치(오늘 기준)보다 저렴하다면 해당 주식을 매수해야 합니다.
다음은 위의 예에서 현재 가치에 대한 자세한 분석입니다.
| 연도 | 미래 가치(FV) – 루피 | 공식- | 현재 가치(PV) – 루피 |
| 0 | 0 | 0 | 0 |
| 1 | 10 | PV =FV / [1 + 0.15]^1 | 8.7 |
| 2 | 10 | PV =FV / [1 + 0.15]^2 | 7.56 |
| 3 | 10 | PV =FV / [1 + 0.15]^3 | 6.58 |
| 4 | 510* | PV =FV / [1 + 0.15]^4 | 291.59 |
| 총계 | 314.43 |
*4년차에 미래 가치는 배당금에 매도 할인가를 더한 금액(예:Rs 10 + Rs 500 =Rs 510)이 됩니다.
여기서 구매 가격은 Rs 313.43 미만이어야 합니다. 연 15%의 연간 수익률을 얻고 싶다면(연간 10루피의 일정한 배당금과 4년차 말에 500루피의 판매 가격을 가정).
이것은 주식의 가치를 평가하기 위해 어떻게 화폐의 시간 가치(TVM) 개념을 사용할 수 있는지에 대한 가장 간단한 예입니다. DCF(Discounted Cash Flow) 분석과 같은 주식 가치 평가 방법론에서 NPV(순현재가치)를 구할 때도 동일한 개념이 사용됩니다.
또한 읽어보세요
화폐의 시간 가치(TVM)는 금융의 기본 개념 중 하나입니다.
오늘 손에 있는 루피가 미래에 받게 될 루피보다 더 가치가 있다고 명시되어 있습니다. 오늘 또는 내일 돈을 버는 선택이 주어진다면 항상 첫 번째 옵션을 선택하십시오.
또한 TMV는 기간, 이자율 및 연간 복리 기간 수의 세 가지 요소에 따라 달라집니다. 기간, 이자율 및 연간 복리 기간이 높을수록 화폐의 미래 가치가 높아집니다.
이제 주식 시장의 최신 업데이트를 받을 수 있습니다. 트레이드 브레인 뉴스 그리고 우리의를 사용할 수도 있습니다. 트레이드 브레인 포털 좋아하는 주식에 대한 기본 분석